|
Die totale Differentiation und was sie ökonomisch bedeutet
06.10.2003
(VS) In der Ökonomie werden Sachverhalte gerne mit Hilfe der Mathematik analysiert. Oft wird das Mittel der totalen Differentiation aus der Analysis verwendet. Es soll anschaulich erklärt werden, was diese Methode real bedeutet.
Die Ausgangslage beruht darauf, daß es eine Größe (Hauptgröße) gibt, die sich verändert hat, d.h. es gibt für diese Größe ein vorher (a priori) und ein nachher (a posteriori). Der Ökonom betrachtet diese Veränderung a posteriori mit einem Gleichungssystem, auf dessen linker Seite die Veränderung der Hauptgröße aufgrund deren Erklärungsvariablen steht, d.h. denjenigen Einflussgrößen, die auf die betrachtete Größe eingewirkt haben, und auf deren rechter Seite diese einflussgrößenabhängige Veränderung der Hauptgröße, d.h. die bezogen auf die einzelne Einflussgröße veränderte Hauptgröße, gewichtet mit der Veränderung durch die Einflussgröße im einzelnen steht.
Diese etwas umständliche verbale Erläuterung sieht als mathematische Formel so aus:
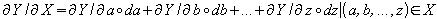
Die Hauptgröße sei Y und die Einflussgrößen hierauf seien alle Elemente aus X, d.h. hier alle Kleinbuchstaben von a bis z; die Anzahl der Einflussgrößen sei zunächst ohne besonderen Grund auf 26 beschränkt. Das Leibniz-d stehe für eine Veränderung, die mit der jeweils dahinterstehenden Größe geschehe; es wird zunächst davon ausgegangen, daß diese Veränderung gegeben sei. Der Kleinbuchstabe d meint ebenso die Veränderung der dahinterstehenden Größe (Einflussgröße), jedoch als Gewicht die Änderung beschwerend.
Ein Beispiel soll diesen Sachverhalt deutlich machen:
Angenommen, unsere Hauptgröße sei das Wetter, das mit Y bezeichnet sei. Mit Y meinen wir einen vollkommen durchschnittlichen Tag in der BRD, insbesondere seien die drei Einflussgrößen Regen, Bewölkung und Wind durchschnittlich und es gebe nur diese drei, die für das Wetter bestimmend seien. Unser Wetter Y habe dabei folgende unabhängige Werte für die drei Einflussgrößen: Regen 20; Bewölkung 7; Wind 30. Was die einzelnen Zahlen genau zu bedeuten haben, d.h. ihre Dimension, sei hier irrelevant. Der Einfachheit halber sei die Dimension der Einflussgrößen gleich, d.h. Regen sei nicht 20%, Wind 30 km/h, Bewölkung 7 irgendwas, sondern es handle sich bei allen dreien um die Dimension lambda. Wäre die Dimension Euro, dann hätte Regen 20 Euro, Bewölkung 7 Euro und Wind 30 Euro, was immer das bedeuten würde. Hier jedoch sei sie lambda, ein Umrechnungsfaktor, den wir an anderer Stelle irgendwie ermittelt haben. Es sei bekannt, daß sich a posteriori die Werte der Einflussgrößen auf folgende verändert haben: Regen 20; Bewölkung 4; Wind 55. Wir wissen jedoch nur formal, wie stark sich diese Änderungen auf das Wetter auswirken; vereinfachend nehmen wir hier an, daß die Einflussgrößen sich summerisch auf das Wetter auswirken.
|
Beispiel:
Es wird für das Beispiel angenommen, dass das Wetter beschrieben werden kann durch die Funktion: Y = (0,5r + 0,2b + 0,3w).
Das aktuelle Wetter sei gekennzeichnet durch die Einflussgrößen:
Regen 20; Bewölkung 7; Wind 30
Für das quantifizierte Wetter ergibt sich:
Y=(0,5*20+0,2*7+0,3*30) = 20,4
Das Wetter hat sich verändert zu:
Regen 20; Bewölkung 4; Wind 55.
Nach Einsetzen der Werte ergibt sich:
Y=(0,5*20+0,2*4+0,3*55)=27,3
Nominal haben die Änderungen der Einflussgrößen folgenden Einfluss auf die Wetteränderung:
Regen:
Anteil 50 %, Änderung dr=0,
Einfluss: 0,5*0=0
Bewölkung:
Anteil 20 %, Änderung db = -3,
Einfluss: 0,2*(-3)= -0,6
Wind:
Anteil 30 %, Änderung dw=25,
Einfluss: 0,3*25=7,5
|
|
Insofern die Einflussgrößen aber mehr als ihre Summe sind, also es alle möglichen Relationen gibt, lassen diese sich ohne weiteres funktional darstellen. Mathematisch sei Y eine Funktion, d.h. eine Zuordnungsregel, die angibt, welche Einflussgrößen in welchem Zusammenhang auf das Wetter wirken. Die Funktion Y sei gleich (0,5r+0,2b+0,3w). Unser Y (Wetter) sei somit zu beschreiben aufgrund der Formel (0,5mal20+0,2mal7+0,3mal30), bzw. einfach aus der Summe = 20,4; das sei unser quantifiziertes Durchschnittswetter eines Tages übers Jahr in der BR Deutschland.
Nunmehr wollen wir eine stattgefundene Änderung des Wetters analysieren. Die Veränderung des Wetters 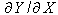 also die Veränderung von Y aufgrund der Veränderung von X (Regen, Wind und Bewölkung) splitten wir nun auf. Wie oben ersichtlich, habe sich der Regeneinfluss nicht verändert. Wenn wir nun mathematisch ermitteln wollen, was dies für das Wetter bedeutet, müssen wir zunächst die also die Veränderung von Y aufgrund der Veränderung von X (Regen, Wind und Bewölkung) splitten wir nun auf. Wie oben ersichtlich, habe sich der Regeneinfluss nicht verändert. Wenn wir nun mathematisch ermitteln wollen, was dies für das Wetter bedeutet, müssen wir zunächst die
|
erste Ableitung der Wetterfunktion 0,5r+0,2b+0,3w (=Y) nach der Einflussgröße Regen (=r) bilden. Nach den Ableitungsregeln ergibt sich 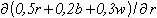 = 0,5. Die Veränderung von Y beruht auf Grund der
summerischen Funktion also zu 50% auf dem Regen. Um dies aktuell genauer zu quantifizieren, müssen wir nach der obigen Ausgangformel die 0,5 nun mit der bekannten Regenänderung dr multiplizieren. Wie wir wissen, hat sich der Regen nicht geändert, womit unser 50%tiger Regeneinfluss mit 0 zu multiplizieren ist, was uns intuitiv einleuchtet. Die weitere Analyse beschäftigt sich mit der Bewölkung, von der wir wissen, daß sie sich von 7 auf 4, also um -3 geändert hat. Auch hier ermitteln wir, was dies für eine Wirkung auf das Wetter hat. Diesmal leiten wir unsere Wetterfunktion nach der Einflussgröße Bewölkung (b) ab. Somit ergibt = 0,5. Die Veränderung von Y beruht auf Grund der
summerischen Funktion also zu 50% auf dem Regen. Um dies aktuell genauer zu quantifizieren, müssen wir nach der obigen Ausgangformel die 0,5 nun mit der bekannten Regenänderung dr multiplizieren. Wie wir wissen, hat sich der Regen nicht geändert, womit unser 50%tiger Regeneinfluss mit 0 zu multiplizieren ist, was uns intuitiv einleuchtet. Die weitere Analyse beschäftigt sich mit der Bewölkung, von der wir wissen, daß sie sich von 7 auf 4, also um -3 geändert hat. Auch hier ermitteln wir, was dies für eine Wirkung auf das Wetter hat. Diesmal leiten wir unsere Wetterfunktion nach der Einflussgröße Bewölkung (b) ab. Somit ergibt 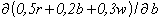 = 0,2 und besagt, daß die Bewölkung 20% Einfluss auf das Wetter hat. Auch hier müssen wir nun wieder die 0,2 mit db multiplizieren, was ergibt 0,2 mal (-3) = -0,6 - somit hat die Änderung der Bewölkung auf das Wetter einen Einfluss von nominal -0,6 gehabt. Betrachten wir nun noch den Wind, von dem wir wissen, daß er sich um 25 verändert hat. Wir leiten unsere Wetterfunktion nach der Einflussgröße Wind (w) ab. Somit ergibt
= 0,2 und besagt, daß die Bewölkung 20% Einfluss auf das Wetter hat. Auch hier müssen wir nun wieder die 0,2 mit db multiplizieren, was ergibt 0,2 mal (-3) = -0,6 - somit hat die Änderung der Bewölkung auf das Wetter einen Einfluss von nominal -0,6 gehabt. Betrachten wir nun noch den Wind, von dem wir wissen, daß er sich um 25 verändert hat. Wir leiten unsere Wetterfunktion nach der Einflussgröße Wind (w) ab. Somit ergibt 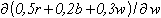 = 0,3 und besagt, daß der Wind zu 30% Einfluss auf das Wetter hat. Wir multiplizieren die 0,3 mit 25, also der Änderung des Windes (dw) und erhalten 7,5 - der Wind hat also einen Einfluss auf die Wetteränderung von nominal 7,5 gehabt. = 0,3 und besagt, daß der Wind zu 30% Einfluss auf das Wetter hat. Wir multiplizieren die 0,3 mit 25, also der Änderung des Windes (dw) und erhalten 7,5 - der Wind hat also einen Einfluss auf die Wetteränderung von nominal 7,5 gehabt.
Wir wissen nunmehr, daß sich unser Wetter Y von einem ursprünglichen Wert von 20,4 auf (20,4+0-0,6+7,5) = 27,3 verändert hat. Auch wissen wir aufgrund unserer Analyse, daß sich die Änderung von insgesamt 6,9 zu (-0,6) aufgrund einer geringeren Bewölkung und zu 7,5 aufgrund stärkeren Windes ergeben hat. Somit können wir die Wirkungszusammenhänge unseres Wetters formal darstellen und begründen. Sicherlich wissen wir deswegen noch nicht, warum die Einflussgrößen so aufs Wetter wirken, jedoch haben wir durch die Analyse einen deutlicheren Einblick in einen komplexen Zusammenhang gewonnen. Gemeinsam mit weiterer empirischer Forschung lassen sich weitere Erkenntnisse gewinnen, so daß letztlich sicherere Prognosen möglich sind. Nachzutragen ist noch, daß es sich in diesem Beispiel um hypothetische Werte handelt, die ohne gültige Transformationsfunktion keinen realen Bezug haben. Außerdem sei die Anzahl der Erklärungsvariablen beliebig erweiterbar und nicht auf die 26 Buchstaben des Alphabets begrenzt.
In der Wirtschaft wird mit dem gleichen Mittel versucht, Aussagen über sie zu machen, insbesondere solche über die Zukunft (Prognose). Schließlich handelt es sich bei der Wirtschaft ebenso wie bei dem Wetter um ein außergewöhnlich komplexes System. Auf beide Phänomene wirken eine gigantische Anzahl von Einflussgrößen, die sich weitgehend der Kontrolle entziehen. Der Unterschied der Wirtschaft besteht darin, daß sie menschengemacht ist und daß bereits heute die Erklärungsvariablen zum Teil beeinflussbar sind, wobei jedoch die Reagibilität der Wirtschaft auf die Einflussgrößen undeutlich ist, zumal diese sich über die Zeit verändern können. In gleicher Weise wie oben beschrieben kann man mit der totalen Differentiation versuchen, Veränderungen a posteriori zu analysieren. Von entscheidender Relevanz sind in einem zu oben vergleichbaren Fall die Koeffizienten der Einflussgrößen, im Beispiel die 0,5; 0,2 und 0,3. Es ist möglich, diese bei einer gegebenen Veränderung der Hauptgröße (Wirtschaft) zunächst statistisch zu schätzen und mit Hilfe von
|
Computern durch zu deklinieren, welche Koeffizienten-Kombinationen das reale a posteriori gemessene Ergebnis erbringt. Hat man die Koeffizienten ermittelt, lassen sich diese a priori anwenden und Aussagen über die zukünftige Wirtschaftsentwicklung machen, insofern sich die Einflussgrößen einzeln oder in Teilmengen gewollt oder ungewollt verändern. Das Problem dabei ist, daß man in der Regel wegen der übergroßen Anzahl nicht alle Erklärungsvariablen kennt. Hinzu kommt, daß die Wirkung von Erklärungsvariablen sich in gewissen Zusammenhängen unbekannt verändern können, z.B. hat eine Flutkatastrophe ungeahnte ökonomische Wirkungen auf einige Erklärungsvariablen. Und so läßt sich weiter konstatieren, daß sich die bekannte mit obigem Mittel erforschte Reagibilität der Wirtschaft auf bestimmte Einflussgrößen über die Zeit ändern kann, sei es kurz- (1 Jahr), mittel- (2-5 Jahre) oder langfristig (6-30 Jahre).
Was wäre nun der Schritt, wenn sich die Änderung ergeben hätte nicht aufgrund der Einflussgrößen und ihrer Koeffizienten, sondern sich innerhalb des Gesamtzusammenhanges eine neue Konstellation, mathematisch also eine neue Funktion Y, vermuten ließe? Auch hier könnte man mit Hilfe von Computerprogrammen errechnen, auf Grund welcher Funktion (obiges Beispiel könnte dann so aussehen: Y=(0,5r+0,2b-0,3w) die gegebenen Einflussgrößen ein a posteriori beobachtetes Phänomen ergeben. Diese Erkenntnis würde man in zukünftige Prognosen einbeziehen und die Rechnung somit der geänderten Realität anpassen.
Absolute Sicherheit ist so gut wie unmöglich: A priori getroffene Aussagen über die Wirtschaft müssen nicht zum richtigen Ergebnis a posteriori führen und sind, wie bei Wetterprognosen, mit Vorsicht zu genießen, insbesondere, weil sog. externe Effekten
|
|
Die Ableitung (Differentiation)
Mit der Ableitung einer Funktion erhält man nähere Kenntnisse über den Zusammenhang von Größen, die aufeinander Einfluss nehmen. Die Funktion ist dabei eine mathematische Zuordnungsregel, die diesen Zusammenhang
repräsentiert. Für die Ökonomie sei hier beispielhaft ein Fall aus der Produktion genannt. Verschiedene Größen (sog. Inputs) ergeben, nachdem sie einen Produktionsprozess durchlaufen haben (z.B. eine Maschine), eine neue Größe (sog. Output), das Ergebnis einer Produktion; solch eine Funktion nennt man ökonomisch Produktionsfunktion.
Nach Beobachtung und Berechnung der Funktion kann man mit dieser (mathematische Formel) errechnen, wieviel Output eine gegebene Menge Input durch die Produktion erbringt, bzw. wieviel Input nötig ist, um eine vorgegebene Menge Output zu erzielen. Die Ableitung einer Produktionsfunktion gibt Auskunft darüber, wie stark der Einfluss eines Inputs auf den Output ist und vice versa. Wenn nicht nur eine Einflussgröße (Maschine=Kapital) hier bestimmend ist, sondern mehrere (Arbeit, Boden, Kapital), so unterscheidet man zwischen totaler und partieller Differentiation. Dabei ist die partielle die Untersuchung des Zusammenhangs nach nur einer Einflussgröße (Arbeit oder Boden oder Kapital) und die totale die Summe der partiellen Ergebnisse. Dabei meint diese Untersuchung die Anwendung von Ableitungsregeln auf die Funktion. Das Ergebnis sind die sog. Ersten Ableitungen partiell oder total. Verwendet man dieselben Regeln auf die Ergebnisse der ersten Ableitung nochmal, so erhält man die zweite Ableitung u.s.f.. Die hier beschriebene totale Differentiation meint aber die Summe der partiellen ersten Ableitungen. Diese erste Ableitung nach einer Einflussgröße sagt aus, wie stark diese einzelne Größe auf das Gesamtergebnis wirkt, bzw. wie sehr sie in der Betrachtung für dieses Ergebnis verantwortlich ist.
|
(z.B. Flutkatastrophe, außerdeutsche Einflüsse anderer Staaten oder Staatengemeinschaften) unvorhersehbar sind. Mit Hilfe wahrscheinlichkeitstheoretischer Methoden und Schätzwerten läßt sich aber die Güte der Prognose, also deren Sicherheitsgrad, näher beleuchten. So gewonnene rationale Erkenntnisse lassen sich als Grundlage für die Entscheidungsfindung in der Wirtschaftspolitik nutzen, womit zumindest nach der Vernunft alles Menschmögliche getan wurde, die richtige Entscheidung zu treffen.
Die hier beschriebene Methode der totalen Differentiation ist nur eine mathematische Methode zur ökonomischen Beleuchtung der Wirklichkeit.
Diskutieren Sie über dieses Thema im Newsatelier-Forum.
Hauptseite Gesellschaft
|
